Part A Determine the magnitude of the electric field E at the origin 0. To use this online calculator for Radius of Circle given arc angle and arc length enter Arc Length s Angle α and hit the calculate button.
Arc Length Formula How To Find Length Of An Arc Examples
Or 2rh h2 d24.

. The formula for the Radius of an Arch is. Float yAverage y1y220. Using that arc radius angle radians we have.
R 180 l πθ. NOTE The points A B and C must not be in the same line. Halfway point float xAverage x1x220.
It takes radians a little more than radians to make a complete turn about the center of a circle. The formula for the radius of a circle based on the length of a chord and the height is. On a circle of radius r at an angle of θ we can find the coordinates of the point x y CirclesPoints on a Circle at that angle using.
Arc Pi r 2 alpha r sinalpha L r Solving for alpha in the first equation. S is the length of the arc subtended by angle θ. Arc length of the visible circle known L length to edge known Lets assume L 0 Pi the number pi.
An arc can be measured in degrees. Even easier this calculator can solve it for you. Area of sector lr2 ---2 1 2 225 15 r2 225 215 r.
Area of sector 225 cm 2 ---1 Arc length 15 cm. Express your answer in terms of the variables λ Question. R L2 8h h 2 r L 2 8 h h 2.
So radius of the circle. That would be the radius of you circle. Hence as the proportion between angle and arc length is constant we can say that.
As circumference C 2πr L θ 2πr 2π L θ r. In the diagram above the part of the circle from B to C forms an arc. Alpha arc 2 r - Pi 2 Using that sina - b sinacosb - cosasinb.
The arc subtends a total angle 2θ0 symmetric about the x axis as shown in the figure Figure 1. R c2 8 h h 2 r c 2 8 h h 2. A useful application of the math construct is in construction where the formulas computes the radius of an arch.
The part of the arc that lies above halfway along this line is now a third point draw a line vertically down from this point. R radius. So radians are the constant of proportionality between an arc length and the radius length.
In the circle above arc BC is equal to the BOC that is 45. An arc is a part of a circle. R is the radius of circle A.
We know that for the angle equal to 360 degrees 2π the arc length is equal to circumference. You have to check this before you execute the Steps 1 to 3. A thin rod bent into the shape of an arc of a circle of radius R carries a uniform charge per unit length λ.
This can also be used to trace lines for painted arches as in the photograph of arches painted on a barn door Special thanks to my friend Austin. Do you want to solve for. You always need another piece of information just the arc length is not enough - the circle could be big or small and the arc length does not indicate this.
Find the radius of the sector of area 225 cm 2 and having an arc length of 15 cm. R radius of arch. R is the radius of a circle.
Up to 10 cash back Find the arc length of a circle with circumference that goes from to around its center. L is the length of the chord. So the radius of sector is 30 cm.
It will help to be given the sector angle. Now draw a third line from one of your two original points to the new one drawn on the arc the angle this new. Now from intersecting chords theorem h 2r-h d22.
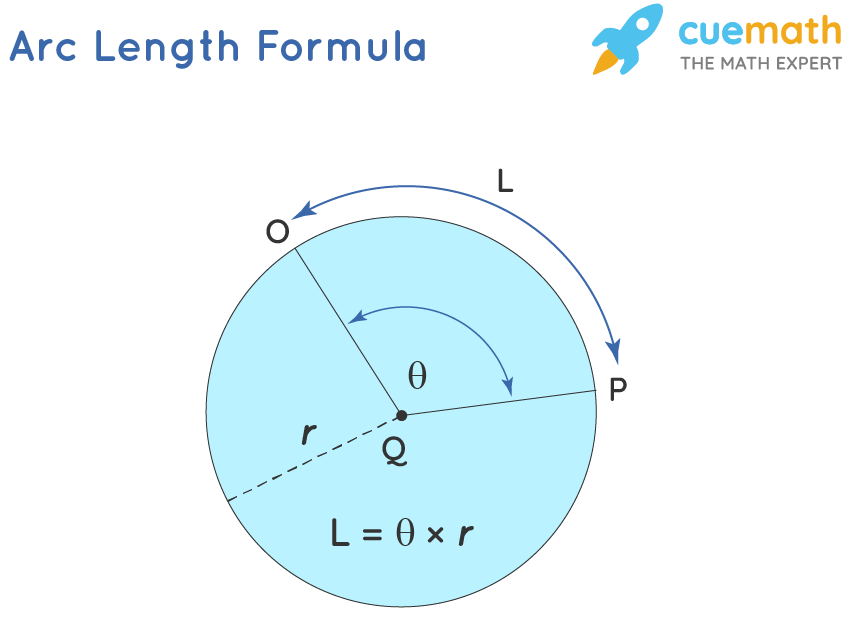
The length of an arc depends on the radius of a circle and the central angle θ. X rcosθ y rsinθ On a unit circle a circle with radius 1 x cosθ and y sinθ. The point you will find would be the center of the circle you want.
Calculate the distance of one of the three points from the center you found on Step 2. Circle center float xCenter sqrtradiusradius - distancedistance40 y1-y2 distance. Where is angle made by connecting the radius to the two ends of the arc given in radians.
Now the diameter DC bisects the chord AB in two halves each having length d2. A thin rod bent into the shape of an arc of a circle. If you have the sector angle θ and the arc length l then you can find the radius.
Orient the two points to lie on the horizontal just makes description easier and draw a line between them. Also the diameter is divided by the chord in two parts the part inside arc h and the remaining 2r-h. Coordinates of the point on a circle at a given angle.
This makes sense because the full circumference of a circle is. R 30 cm. L θ C 2π.
GLuint createArc float x1 float y1 float x2 float y2 float radius bool arcDirection bool useBiggerArc distance between points float distance sqrtx1-x2x1-x2 y1-y2y1-y2. H is the height of the chord. So r d28h h2.
A tangent is. The radius is half the length of the diameter. Point B is any point on the circle and is described by the rectangular coordinates x y.
Here is how the Radius of Circle given arc angle and arc length calculation can be explained with given input values - 0763944 2431415926535892. A tangent is a line that touches a circle at only one point. Arc length radius central angle radians arc length circumference central angle degrees 360 where circumference 2 π radius Knowing two of these three variables you can calculate the third.
Remember that arc length of a circle is given by.

Radians As Ratio Of Arc Length To Radius Circles High School Geometry Khan Academy Youtube


0 Comments